1.
Punto: El punto es el elemento base de la geometría, ente fundamental,
porque con él determinamos las rectas y los planos. Podemos definirlo también,
como la intercesión de dos líneas. Sirve para indicar una posición y no tiene
dimensión.
2.
Línea: Se trata, para la geometría, de
una seguidilla de puntos que se extiende indefinidamente y de manera continua
en una única dimensión.
3.
Línea Recta: es una sucesión de puntos y éstos carecen de
magnitud, pero se considera como una trayectoria de puntos que no cambian de
dirección
4.
Semirrecta: Si se tiene una recta con un punto P contenido en
ella y que la divide, cada una de las porciones en que queda dividida se le
conoce como semirrecta.
5.
Segmento
de línea recta: es una secuencia de puntos de rectilíneos que
tiene un punto de origen y un punto final. En
este caso se origina en A y finaliza
en B.
6.
Angulo: Ángulo es la porción de plano limitada por dos
semirrectas con origen en un mismo punto. Las semirrectas se llaman lado
inicial y final. Al origen común se le denomina vértice del ángulo.
Grado: un grado es la separación que existe entre dos
líneas.
Minuto: Un minuto
de arco, denominado también minuto
sexagesimal, es una unidad del ángulo plano frecuentemente utilizada en
artillería, astronomía y otras disciplinas, equivalente a 1/60 de un grado
sexagesimal.

Segundo:
El segundo es
una unidad ángulo utilizada en
Astronomía que equivale a 15 segundos sexagesimales o 1/4 de minuto
sexagesimal. Equivale al ángulo que
gira la Tierra en el lapso de 1 segundo.
7.Clasificacion de angulos segun sus medidas:
a) Ángulo recto: Mide exactamente 90°
b) Ángulo agudo: Mide menos de 90°
c) Ángulo obtuso: Mide mas de 90°
d) Ángulo llano: Mide exactamente 180°
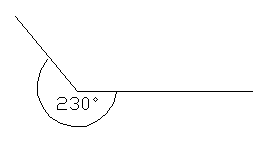
e) Ángulo entrante o cóncavo:Un ángulo Cóncavo es el que mide más de 180° pero menos de 360°
f) Ángulo perígono: mide 360° exactos
8) Otra clasificación de los ángulos según su posición es:
a) Opuestos por el vértice: Son angulos que tienen un vertice comun, los angulos de uno son prolongacion de los lados del otro dando asi que tengan la misma medida
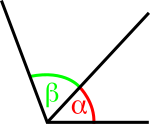
b) Adyacentes:Aquellos que tienen el mismo vértice, un lado en común entre sí y los lados no comunes forman parte de una misma recta
c) Complementarios:
Ángulo que sumado a otro forma uno de 90 grados.

d) Suplementarios:Ángulo que sumado a otro forma uno de 180 grados
9) Triángulo:El triángulo es un polígono de tres lados que da origen a tres vértices y tres ángulos internos.
10) Clasificación de los triángulos por sus lados.
un triángulo pude clasificarse en equilátero, donde los tres lados del triángulo son iguales.
en isósceles, el triángulo tiene dos lados iguales y uno desigual.
y en escaleno, donde el triángulo tiene los tres lados desiguales.
11) Clasificación de los triángulos por sus ángulos.
se pueden clasificar según la medida de sus ángulos, puede ser un acutángulo, donde los tres
ángulos son agudos; es decir, ángulos menores que 90°.
Si un triángulo presenta un ángulo recto o ángulo de 90° se dice que es rectángulo
y si presenta a uno de los tres ángulos como obtuso; es decir, un ángulo mayor que 90° se considera como obtusángulo.
12) Rectas y puntos notables en el triángulo:
En
un triángulo se definen cuatro tipos de
rectas denominadas, genéricamente, rectas
notables.
Esas rectas son:
mediatrices:Es la recta perpendicular a dicho lado que pasa por el punto medio (o centro) de éste.
bisectrices:La bisectriz de un triangulo es el segmento que, dividiendo uno de sus tres ángulos en dos partes iguales, termina en el correspondiente lado opuesto.
medianas
alturas:Altura es cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).
En un triángulo tendremos tres rectas de cada tipo.
Los
puntos de intersección de dichas rectas se denominan puntos
notables y son,
respectivamente:
circuncentro
incentro:Es el punto de corte de las tres bisetrices.Es el centro de una circunferencia inscrita en el triángulo.
baricentro:Es el punto de corte de las tres medianas.
El baricentro divide a cada mediana en dos segmentos, el segmento
que une el baricentro con el vértice mide el doble que el segmento que
une baricentro con el punto medio del lado opuesto.
ortocentro:Es el punto de corte de las tres alturas.
13) Polígonos:La palabra poligono proviene del griego y significa "muchos angulos", los polinomios son figuras planas y tienen de 3 a mas lados
14) Rectas y segmentos enuna Circunferencia:Las rectas y segmentos de una circunferencia son:
Radio: el radio de una circunferencia es cualquier segmento que une el centro a cualquier punto de dicha circunferencia.
Diametro: El diámetro de una circunferencia es el segmento que une dos puntos de la circuferencia
y pasa por el centro.
Cuerda:La cuerda
es un
segmento que une dos puntos de la circunferencia.
Tangente:La recta tangente o también llamada recta exterior a una circunferencia de centro O que pasa por un punto T de la misma es la recta perpendicular al radio
Secante:Son denominadas rectas secantes aquellas rectas que cortan una circunferencia en dos puntos determinados.
Arco:Un arco de circunferencia
es cada una de las partes en que una cuerda divide a la circunferencia.
15) Ángulos en una circunferencia.
Ángulo central :es el ángulo que tiene su vértice en el
centro de la circunferencia y los lados son radios de ella
Angulo inscrito: es aquel que tiene su vértice en
la
circunferencia.
Angulo interior, tiene su centro en un punto interior del
círculo.
Angulo Exterior es aquel que
tiene su vértice en un punto exterior de la circunferencia, pudiendo ser sus lados, tangentes o secantes a
la misma.
16) El símbolo de congruencia: la cogruencia se denota con el signo:
17) Congruencia de triángulos: